) is used for the distance between crests, or the "wavelength". Key points: wave-particle duality; interference; temperature; inverse r squared law; luminosity; the electromagnetic spectrum
Most of what we know about astronomy has been learned by studying light, so
it is important to understand how it behaves. Light is a form of electromagnetic radiation, vibrating electric and
magnetic fields moving through space. The Greek letter lambda () is used for the distance between crests, or the "wavelength".
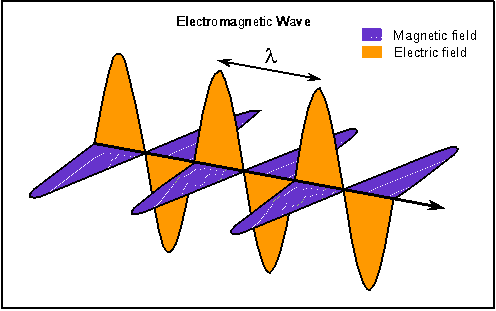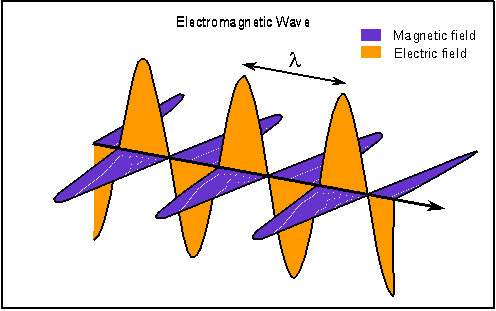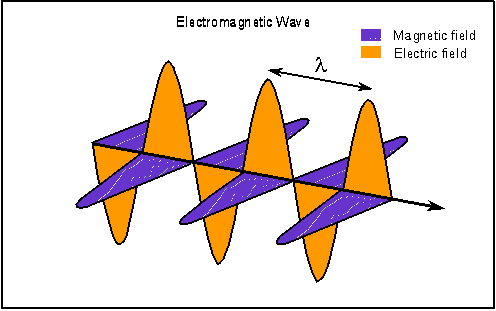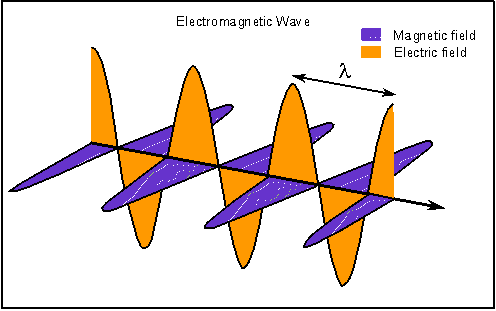
(From Nick Strobel, www.astronomynotes.com)
Light is also a form of fundamental particle, called a photon. That is,
Light has "wave-particle duality"
1. Diffraction
  |
When light encounters a barrier, such as a slit, its path bends and it can illuminate areas behind the slit that are larger than the width of the slit. Here are water waves at a breakwater; diffraction causes the semi-circular pattern behind the breakwater (to left, from http://www.exploratorium.edu/) and diffraction in action to right.(animation by G. Rieke) |  |
2. Interference
 |
How interference works: the black wave is the sum of the blue and green ones. When the blue one is "in phase" with the green, they interfere constructively and the black one is larger than either. When the blue one is "out of phase", they interfere destructively and cancel each other out; the black wave vanishes. (animation by G. Rieke). |
 |
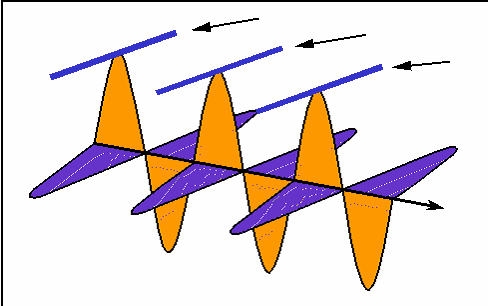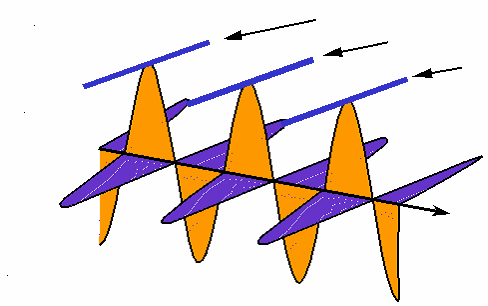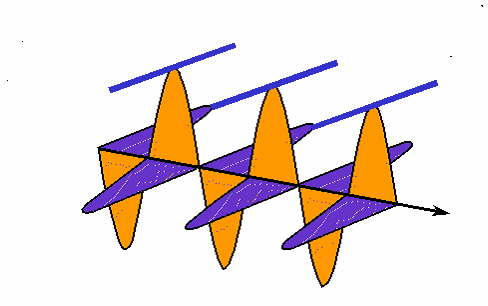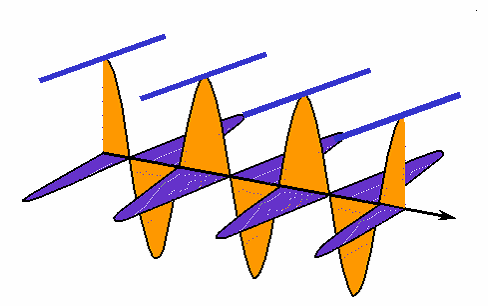Rather than drawing the curvy lines for a wave, sometimes we just draw a straight line for the wave crest seen from the top. |
 |
Here is how the interference animation transfers to this version. (by G. Rieke). |
 |
Many experiments show that light interferes with itself, a general property of waves. Here is an example with water waves, created at two spots. The picture shows how they add and subtract to create a complex pattern of ripples.This process is interference. To the right, an animation shows how an interference pattern changes with time. from Tom Holub, http://www.flickr.com/photos/physicsclassroom/galleries/72157625109662093/ and Robert Hauenstein, Oklahoma State http://physics.okstate.edu/hauenst/class/ph2414/suppl/waves2/int.html |  |
We will show the kind of experiment used to see light interference after the discussion of diffraction and particle behavior.
1. Discrete energies
Photons have specific, discrete energies; the shorter their wavelength, the greater the energy (to be discussed below).
2. Isolated arrival times
| Here is a movie of a comet, taken with a device that amplifies low
light levels and shows every photon. Note the grainy appearance, due to the detection of
individual photons from the sky. This appearance results directly from the discrete energy
and isolated arrival times of the photons.
from Peter McCullough, http://www.astro.uiuc.edu/~pmcc/comet/pinhole.html |
 |
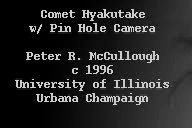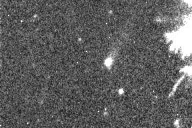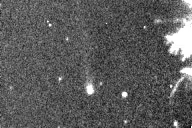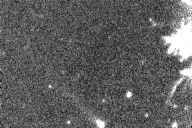Wave-Particle Duality:
If we shine photons one at a time into the box below, we will detect them as discrete particles, each one at a specific position against the back surface. However, if we collect a large number of photons, even one at a time, they will distribute themselves in the "dark" areas and avoid the "light" ones. The "dark" areas are where the positive wavefronts overlap from the two slits letting each photon through. Thus, they result from the combination of diffraction and interference. Perhaps the most curious part is that each photon must pass through both slits! (since we get the pattern even they go through the slits one at a time). This experiment is called "Young's fringes" after the first scientist to do it. Experiment for yourself at http://www.animatedscience.co.uk/blog/wp-content/uploads/focus_waves/rippletank__ripple.html
 |
 |
An image from a real Young's fringes experiment. (from Andrew Boyd, http://www.uh.edu/engines/two_slits-b.jpg) |
If you find this experiment troublesome -- well, so does everyone else
However, it is known to
be a basic aspect of the behavior not only of photons of light, but of all
fundamental particles such as electrons and protons! This topic has become an
entire branch of physics called quantum mechanics.
With changing wavelength, short wavelength to long wavelength, we go from: gamma-rays => x-rays => ultraviolet => visible => infrared => microwave => radio (A nanometer = nm is 10-9 m) (From Hopkins Ultraviolet Telescope Project, http://praxis.pha.jhu.edu/.) |
 |
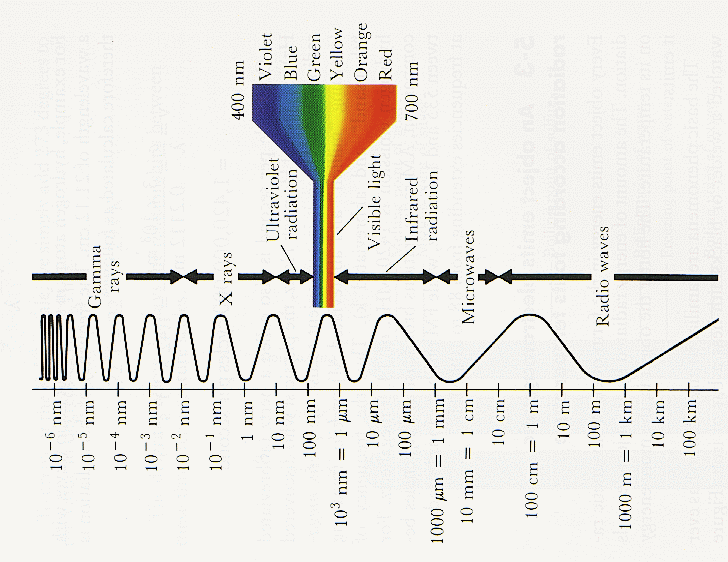These are all forms of “light” or electromagnetic radiation.
The speed of light, c, is a universal constant
c = 3 x 108 meters/sec or c = 3 x 105 kilometers/sec
c = times 
where is wavelength and is frequency. The frequency is the number of wave
crests that pass by a given fixed point per second. From this equation, if we know the
wavelength we can compute the frequency, or if we know the frequency we can compute the
wavelength.
We call a particle of light a photon, so it travels at speed c, obeys the above relationship between wavelength and frequency and it also follows this relation:
E = h times = h = h times c divided by = hc/
where E is energy, h is a constant called Planck’s constant and is frequency.
Thus, if we know the wavelength or frequency, we can compute the energy.
The "Kelvin" temperature scale sets 0 at the lowest possible temperature, where the atomic motions are "stopped" (to the limits set by quantum mechanics). The speed of motion of molecules is proportional to the square root of T(Kelvin) divided by the mass of the molecules.
 |
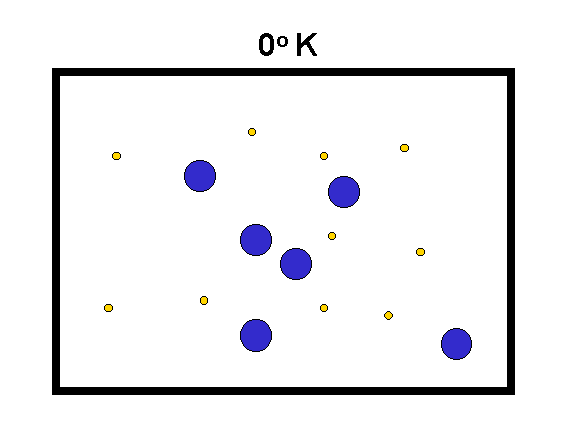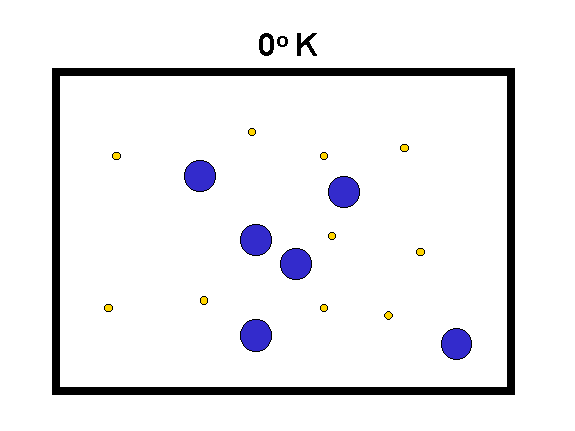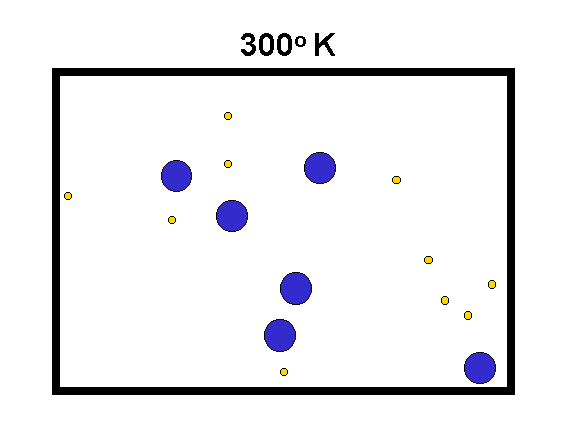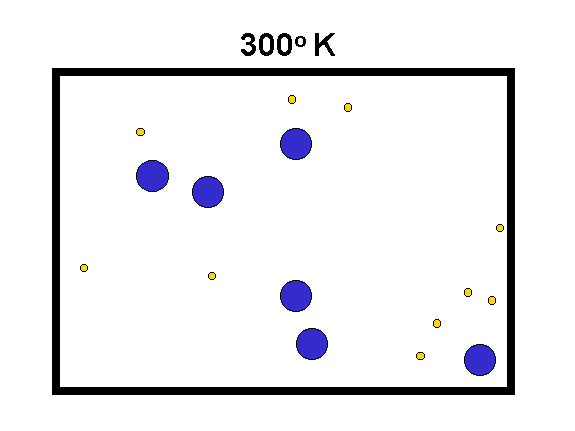We compare hydrogen (yellow, mass = 2) with oxygen (blue, mass = 32) to the left. As the temperature goes up, the speed of the molecules increases (especially for the low mass ones) and they hit the walls of the box harder. Thus, their force on the container walls (the pressure) increases. (animation by G. Rieke) |
Examples: 0o Kelvin = -459o F;
273o K = 32o F = 0o C
Note that Centigrade (or Celsius) degrees are the same size as Kelvin degrees.
Fahrenheit degrees are only 5/9ths as large.
 |
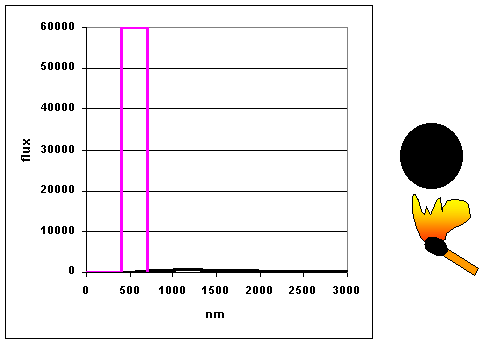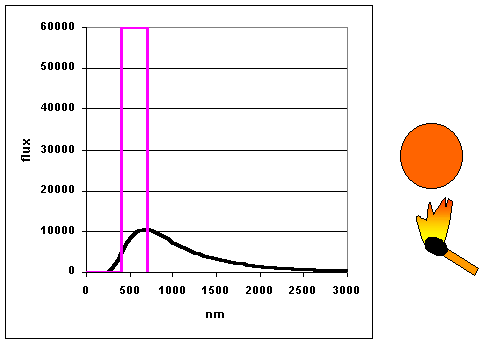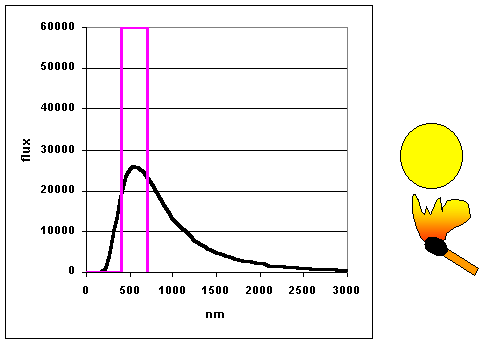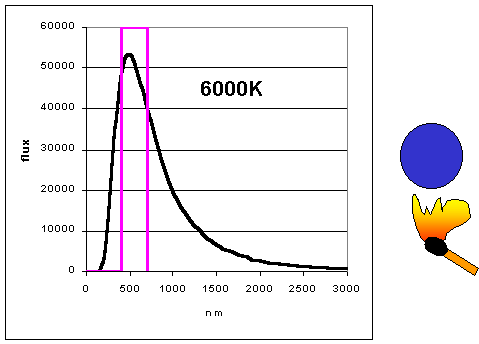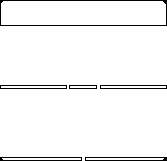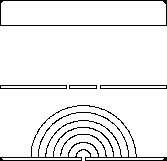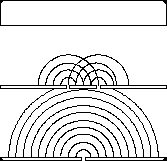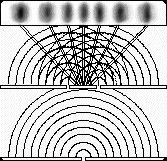
As objects get hotter, they emit more and at shorter wavelengths. (animation
by G. Rieke) The curves as shown to the left are
called blackbody curves – they represent the distribution over wavelength of
the energy emitted by a hot object whose surface would appear perfectly black if it were
cool. Many astronomical objects radiate energy almost as though they were blackbodies.
We now discuss the basic "radiation laws" that describe te behavior of blackbody radiators in physical terms: |
 |
The rapid increase of energy with
temperature is why we can display only a limited range of temperatures in a
"linear" graph like the one above. We can do better with a
"logarithmic" graph where the divisions are in factors of
ten : |
The brightness of a light source (again, it doesn’t matter whether we’re discussing visible light or some other type of electromagnetic radiation) is inversely proportional to the square of the source’s distance from us:
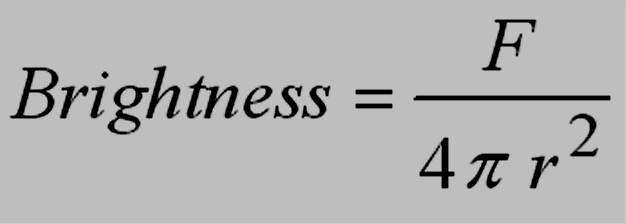
where F = number of photons produced by the source and r = object’s distance
 |
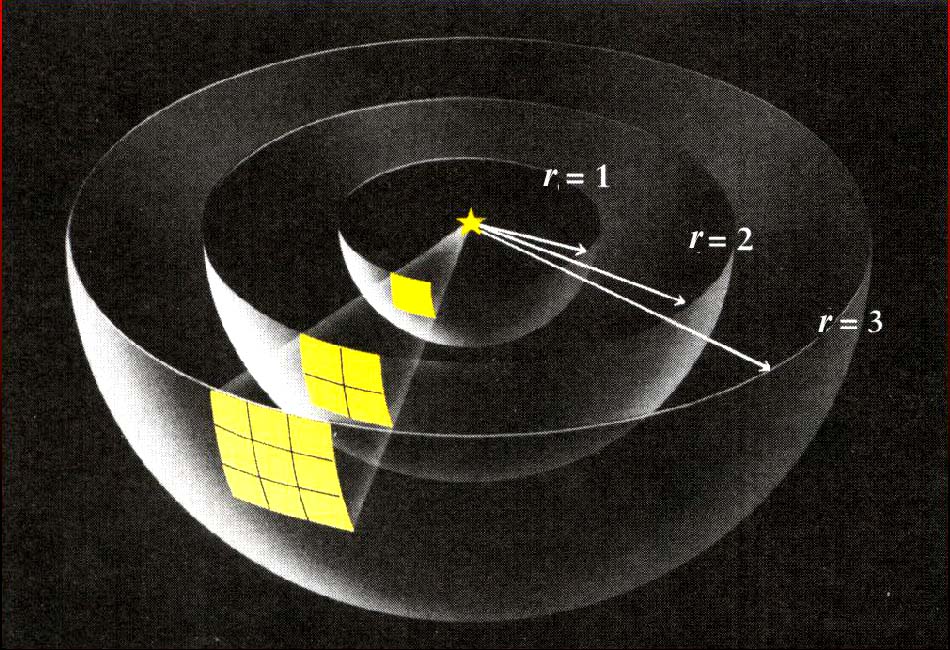This equation follows from the area of a sphere centered on
the source,  . If the brightness fell off with distance slower than , photons would have to be created in empty space to add to those
from the source. If it fell off faster, then photons would have to disappear into empty
space. (From Clem Pryke, http://find.uchicago.edu/~pryke/compton/flyer.html) |
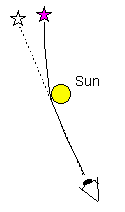
Light is attracted by gravitational fields.
According to Einstein's theory of relativity, light is attracted by
gravitational fields. This effect was originally confirmed by observing the apparent shift
in the positions of stars as their light grazed the limb of the sun, but is now observed
in many other situations. Animation from Firstscience.com, http://www.firstscience.com/site/articles/einstein.asp |
 |
 |
What are the key aspects of electromagnetic radiation
 |
|
Rainbow, from http://www.lioncrusher.com/ecard/ |
Click to return to syllabus |
||
| Click to return to Physical Laws | hypertext |
Click to go to Spectroscopy |
AT4 
=
2,900,000/T
G. H. & M. J. Rieke