
Astronomy is a unique science in that astronomers generally cannot perform experiments or touch the objects of their research. They must learn everything from the light received from planets, stars, and galaxies. Hence understanding light and its interactions with matter is of paramount importance to the astronomer.
Visible light and all other forms of electromagnetic radiation are waves comprised of oscillating electric and magnetic fields traveling through space with a velocity c = 300,000 km/sec.

Note that the electric and magnetic fields are perpendicular to each other and to the direction in which the wave is moving! The amplitudes of the E and B fields are related by E = c B.
Light has four fundamental properties:
= c/n in a medium with refractive index n
Useful relations:
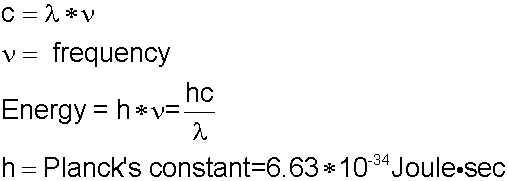
The Electromagnetic Spectrum
|
Spectrum of Electromagnetic Radiation |
||||
|
Region |
Wavelength |
Wavelength |
Frequency |
Energy |
|
Radio |
> 109 |
> 10 |
< 3 x 109 |
< 10-5 |
|
Micro-wave |
109 - 106 |
10 - 0.01 |
3 x 109 - 3 x 1012 |
10-5 - 0.01 |
|
Infrared |
106 - 7000 |
0.01 - 7 x 10-5 |
3 x 1012 - 4.3 x 1014 |
0.01 - 2 |
|
Visible |
7000 - 4000 |
7 x 10-5 - 4 x 10-5 |
4.3 x 1014 - 7.5 x 1014 |
2 - 3 |
|
Ultra-violet |
4000 - 10 |
4 x 10-5 - 10-7 |
7.5 x 1014 - 3 x 1017 |
3 - 103 |
|
X-Rays |
10 - 0.1 |
10-7 - 10-9 |
3 x 1017 - 3 x 1019 |
103 - 105 |
|
Gamma Rays |
< 0.1 |
< 10-9 |
> 3 x 1019 |
> 105 |
The notation "eV" stands for electron-volts, a common unit of energy measure in atomic physics.
1 eV = 1.6x10-19 Joules
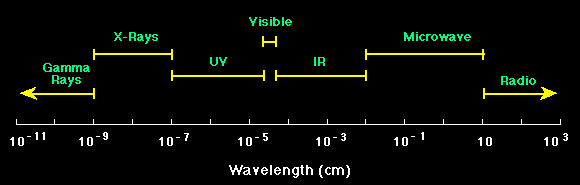
A graphical representation of the electromagnetic spectrum is shown in the figure below.
 |
|
The electromagnetic spectrum |
Thus we see that visible light and gamma rays and microwaves are really the same things. They are all electromagnetic radiation; they just differ in their wavelengths.
Light can behave as either a particle (especially true for highest energy portion of the electromagnetic spectrum) or as a wave (most noticeable at lower energies = longer wavelengths).
The wave character of light leads to interference when two sources of light are observed:
If wave crests match up = constructive interference
(see sum of the light waves)
If wave crests are out of phase = destructive
interference
(see no light)

The electric field of the light wave can be
represented as
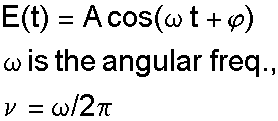
If we sum two light waves
![]()
At time t =0, ![]() 1=0, A1=A2, look at the ETotal for various choices of
1=0, A1=A2, look at the ETotal for various choices of ![]() 2:
2:
| j 2 | Wave 1 | Wave 2 | ETotal |
| 0 | A | A | 2A |
| 45° | A | A/ |
A(1+ |
| 90° | A | 0 | A |
| 135° | A | - A/ |
A(1- |
| 180° | A | -A | 0 |
The interference of light causes many effects including diffraction and is the basis for many astronomical instruments including diffraction gratings and interferometers where several telescopes are coupled together to synthesize the capability of a much larger telescope.
Interference due to two points sources of light:
S1 and S2 are far way from P so the two angles indicated as above are equal (this is called the far-field approximation). Notice the following about this figure:
Difference in distance between P and S1 and S2:
If the light from S2 travels an integral number of wavelengths over this difference, the light from both points will arrive at P with crests matching (e.g., in phase) and will interfere constructively. If the light from S2 travels a half-integer number of wavelengths over the difference, the waves will be out of phase and will interfere destructively: (N is an integer)
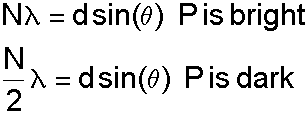
You can see that for a fixed distance d, the brightness at P will depend on the wavelength of the light. An extrapolation of this result explains how a diffraction grating works -- a grating is essentially a series of lines that act like light sources (the S1 and S2 above) so that the light that is transmitted to a distant screen (P above) will have brightnesses at different locations proportional to the brightnesses at different wavelengths in the incoming beam of light.
Photometric Concepts
Measuring brightnesses of stars and galaxies is essential for an astronomer. To follow the discussion below, we also need to understand a unit that astronomers often use for measuring distances, the parsec. A parsec = 3.086x1016 meters.
This is not an arbitrary definition but is based on the concept of parallax and the size of the Earth's orbit.
Units of distance in astronomy
 A hierarchy of distance scales are used by astronomers.
A hierarchy of distance scales are used by astronomers.
Within the Solar System, the radius of the Earth can be used to measure "horizontal parallaxes" as shown on the left. The smallest unit used by astronomers (other than standard physical units like meters) is the astronomical unit, AU, which is the distance of the Earth from the Sun, ~1.5x108 km.
A larger unit, the parsec, is defined at the distance at which 1 AU subtends 1 arc sec, 3.086x1013 km. Larger units like kiloparsecs or even megaparsecs are also used.A light year, the distance light travels in one year = 9.46x10>12 km or ~1/3 parsec, is sometimes quoted but not generally used in professional astronomical work.
|
|
|

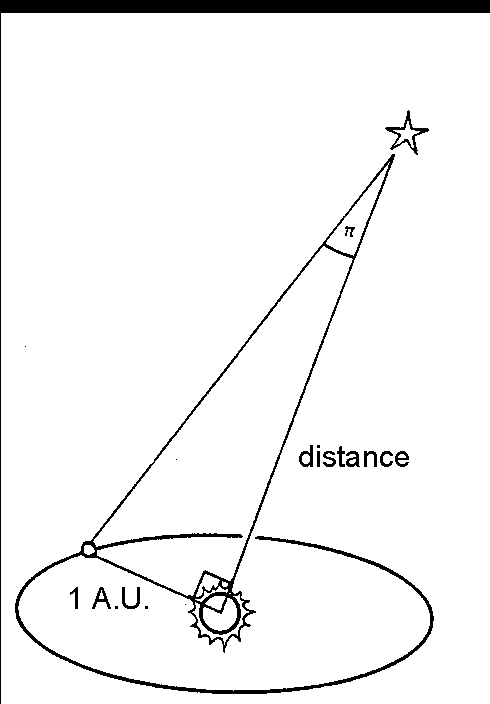

(1"=1/206265 radians so 1 pc =206265 AU = 206265 x 1.496x108km = 3.086x1013km).
Fluxes, Luminosities, and Distances
Consider a surface through which some radiation is passing in a particular direction.
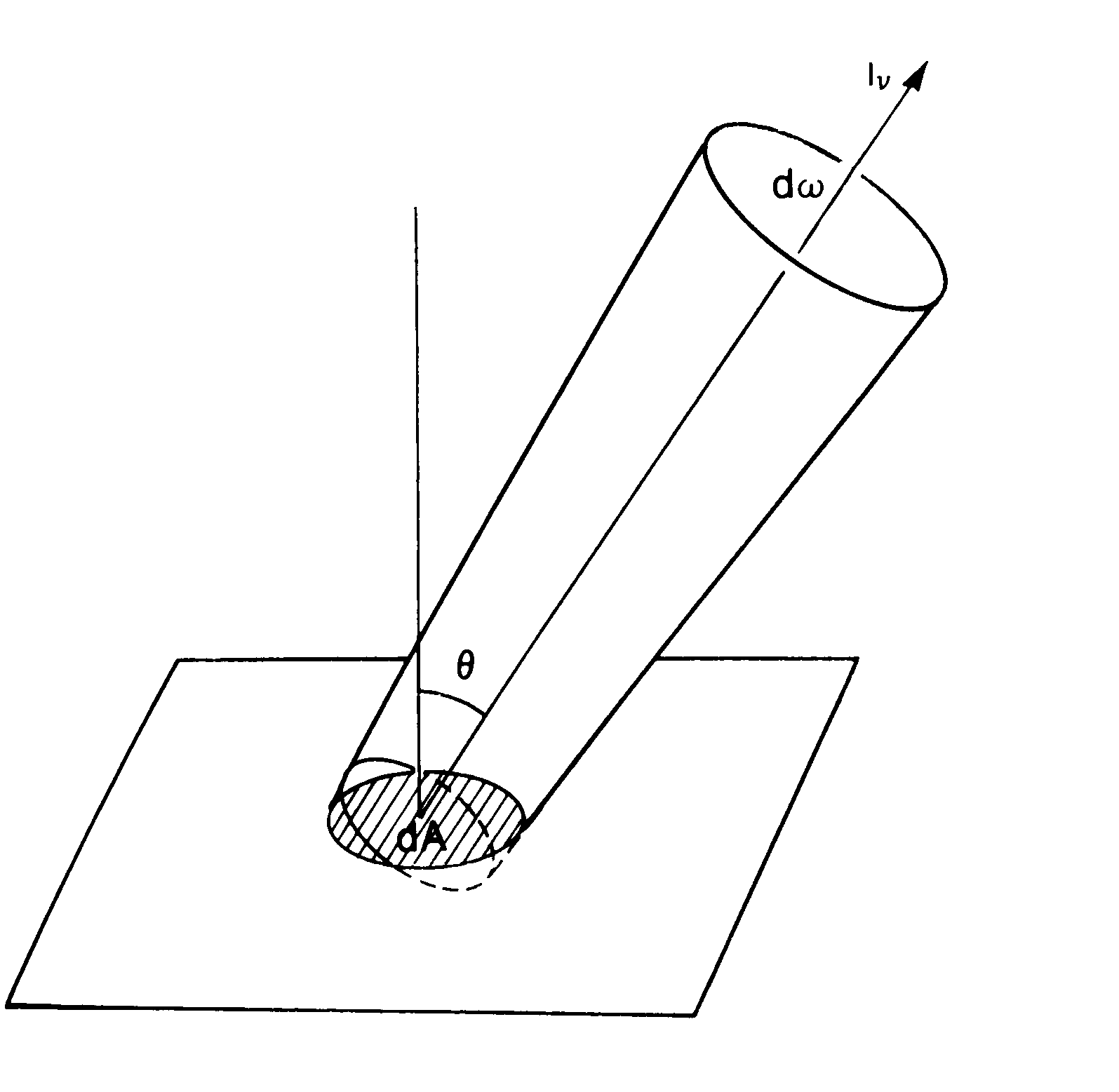
I![]() = specific intensity measured in watts/m2/Hz/steradian
= specific intensity measured in watts/m2/Hz/steradian
(recall that the size of a solid angle is measured in steradians; this part of the definition specifies the direction of the radiation). The intensity depends on the direction and on the solid angle the radiation moves through.
Astronomers usually integrate what is seen over some solid angle so we usually measure "flux" or "flux density" in units of watts/m2/Hz denoted as F![]() . A flux is then the amount of radiation passing through a plane in our direction. See Figure 4.3 and Table 4.1 in the text for a comparison of intensity and flux. Because we cannot resolve the surfaces of stars (other than the Sun!), astronomers are mainly concerned with fluxes when observations are being considered.
. A flux is then the amount of radiation passing through a plane in our direction. See Figure 4.3 and Table 4.1 in the text for a comparison of intensity and flux. Because we cannot resolve the surfaces of stars (other than the Sun!), astronomers are mainly concerned with fluxes when observations are being considered.
Note that "Brightness" is sometimes used casually to mean flux.
The luminosity of a source is the total flux emitted by an object integrated over the object's surface:

We can also define L over limited ranges of wavelength or frequency such as "visual luminosity"; bolometric luminosity means the total integrated over all wavelengths.
The flux that we measure at Earth from an object depends on its distance from us:
d= distance from Earth
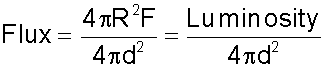
We will try to stick to a convention where R=radius of an object, d=its distance.
Example 1:
A star located at a distance of 10pc has a flux of 0.2 Jy. An identical star is located at a distance of 20pc. What is its flux?
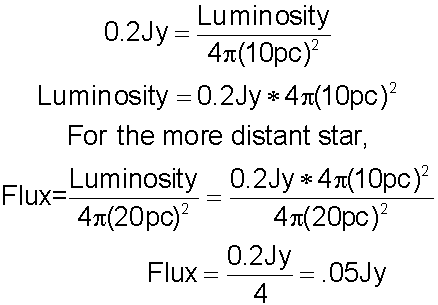
Example 2:
The Sun's luminosity at a particular frequency is 2.8x108 watts/Hz. If it were located at a distance of 4 pc, what would be its flux in Jy?
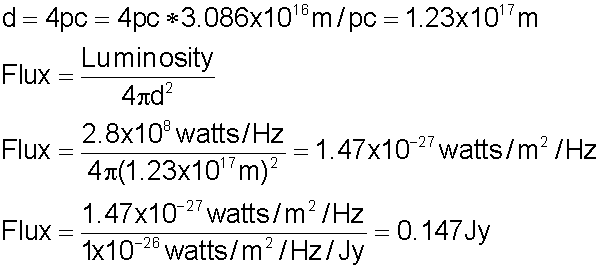
In quantum mechanics you will learn how to derive the following law which we will accept as correct (the text gives a partial derivation). If a perfectly black object is heated to some temperature T, it will emit radiation distributed across the spectrum according to the Black Body Law, also known as Planck's Law:
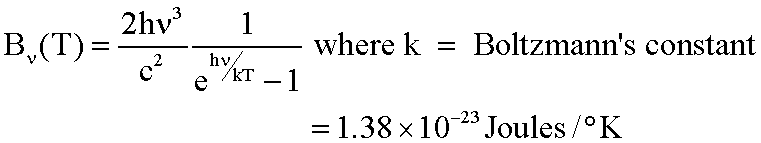
The units of ![]() are watts/unit area/
are watts/unit area/![]() /solid angle, e.g.,
/solid angle, e.g., ![]() is the energy flux leaving a unit surface area in unit frequency interval in a given direction. It is also possible to express the Black Body Law in wavelength units where the units of
is the energy flux leaving a unit surface area in unit frequency interval in a given direction. It is also possible to express the Black Body Law in wavelength units where the units of ![]() are watts/unit area/
are watts/unit area/![]() /solid angle. To convert between forms requires differentiating the Black Body function with respect to either wavlength or frequency and remembering
/solid angle. To convert between forms requires differentiating the Black Body function with respect to either wavlength or frequency and remembering ![]() so .
so .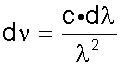
==> We will always use the frequency form in this class.

If we compute 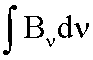 , we will be computing the total energy flux emitted per unit area per unit time; this relation is known as the Stefan-Boltzmann Law:
, we will be computing the total energy flux emitted per unit area per unit time; this relation is known as the Stefan-Boltzmann Law:
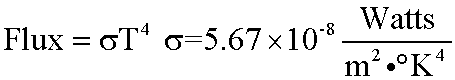
Recall from above that

Most stars radiate sufficiently like a blackbody that this law describes their luminosity quite well.
Let's check how well this works in the case of the Sun:

The actual temperature of the Sun is 5785°K so the Sun is very well approximated by a black body.
If we solve 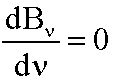 , we will derive Wien's Law which gives us a relationship between the wavelength at which the blackbody curve is maximum and an object's temperature:
, we will derive Wien's Law which gives us a relationship between the wavelength at which the blackbody curve is maximum and an object's temperature:

Since many objects radiate as close approximations to blackbodies, this relation is extremely useful for determining the temperature of a source -- just measure its flux as a function of wavelength and look for the peak. Important note: the relation given above holds for fluxes measured in watts/m2/Hz or other frequency units (meaning per Hz ) . If fluxes are measured in frequency units (meaning per m or nm or micron or Angstrom or other length) then the correct coefficient becomes 2.9x106 instead of 5.1x106
Here's an example:
A star is observed to have a flux of 0.2 Jy in the U filter at 360 nm, 0.4 Jy in the B filter at 440nm and a flux of 0.3 Jy in the V filter at 550nm. Estimate the star's temperature based on these data.
Star's output is maximum at 0.4 Jy at 440nm. Therefore

Doppler Shifts
If a source of electromagnetic radiation is moving, the wavelengths of emitted light will be shifted when observed:

If v is away from the observer, ![]() is positive ("redshifted")
is positive ("redshifted")
and if v is towards the observe, ![]() is negative ("blueshifted").
is negative ("blueshifted").
This relation gives us a handy method for measuring the speeds of sources. In general, Doppler shifts are most easily measured using spectral lines.
