More on Parallax

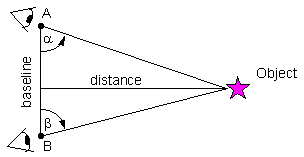
	Surveyors use the same principle to measure distances on Earth
	Distance determination trigonometry: form a triangle with the base of the triangle = the diameter of the earth's orbit and the star being measured at the apex. A star with a parallax of 1" (= 1 arcsec, 1/1800 the diameter of the moon) has a distance of 1 parsec. Distance in parsecs = 1/parallax in arcsecs (Illustration from The Essential Cosmic Perspective, by Bennett et al.)

A star with a parallax of 0.5" is 2 pc distant and so on.

It is very difficult to measure angles smaller than about .01" so until recently this direct distance method was applied only to the nearest stars, those within about 100pc of the earth. With space missions we can do much better, and one is proposed capable of measuring parallaxes to 1 x 10^-5 = 0.00001". This accuracy will let us measure distances directly all the way across the Milky Way galaxy.