Greece and the Birth of Science
The new "Greek" approach to thinking about nature was perhaps the greatest breakthrough ever made in human thought. So far as we can tell, it began about 600 B.C., in Ionia, the southern coast of Asian Turkey, where there were a number of prosperous Greek city-states. Sadly, much of the record is lost (for example, only the first sentence of what is believed to be the first book on science - by Anaximander of Miletus - has survived). Scholars piece the history together from fragments reported by others, frequently centuries after the original writings. From these fragments, though, it is clear that Anaximander, his colleague Thales, and others were raising for the first time broad questions about what unifying themes could explain the behavior of nature.
Astronomy provides only an example of how this new mode of thought sprang forth, but a good one. We can appreciate the advance by comparing with Maya astronomy, which actually came a thousand years after the peak of Greek power and influence, but was independent of them and is a highly developed example of astronomy as it was practiced in other societies prior to the Greeks. In general, as with the Maya, societies that generated enough wealth to invest in a high level of astronomical research were all highly centralized, with a totally dominant ruling class. Astronomy was practiced by an elite society of priests who served the rulers. Astronomy served as a very sophisticated astrology, in which events in the sky were used to forecast the future and help the rulers make critical decisions. The observations were also used to awe the populace, reinforcing the power of the ruling order (as with Stonehenge as well as El Castillo). Astronomy was the province of religion that was part of an oppressive ruling structure.
The Greek civilization had a remarkably different organization, centered on a large number of independent city-states. They had a strong concept of individual rights for the citizens of these states (although ironically, most of the population might be slaves that they had acquired in wars among each other (or with other groups)). Religion was practiced by all of the citizens, any one of whom could go to a temple and make an offering to the appropriate deity. Although there were exceptions, many of the city-states operated on the principle that rulers served the people and did not necessarily rule for life, but could be removed. Thus, the Greek lifestyle ran strongly counter to the oppressive, dominant government/religions that had ruled other wealthy societies.
The combination of efficient farming, the contributions of slaves in doing menial work, the government and religion that responded to the needs of the people, and an efficient social structure that allowed generation of substantial wealth, all worked together to produce a new phenomenon. The Greeks were able to put substantial resources into science, mathematics, philosophy, and literature. Along with these interests came the need to educate, and a teacher class grew up. The most outstanding of these teachers became famous and attracted many pupils to large schools. They thought deeply about nature, mathematics, and philosophy. They left a heritage of important writings on these subjects. Euclid developed virtually the entire subject of geometry and also contributed to optics. Aristotle was a great observer of nature and left many volumes describing the results. Archemides contributed to physics and mathematics. Eudoxus developed a form of calculus. Hippochratus left writings on the practice of medicine, as well as the famous oath that guides all doctors: "Do no harm."
When the city-state structure was threatened, it was forcibly restored. For example, Athens collected contributions from a network of other states to help support its powerful navy in protecting them. Under Pericles, about 430 B.C., these payments grew quickly and the navy was used more to enforce payment than to protect.
|
An Athenian empire quickly came into existence. The wealth taken from
other city-states allowed the great flowering of architecture that we celebrate as one of
the greatest accomplishments of the ancient world, as epitomized by the
Acropolis. (G. Rieke)
|
Sparta and its allies successfully restored the independence of the city-states in the Peloponesian Wars. Athens' imperial ambitions were so immense that it weakened its ability to fight Sparta by invading Sicily in the middle of these wars, where it was disastrously defeated by the navy and army of Syracuse. When the Spartan alliance was finally victorious, they fortunately violated Greek tradition and did not destroy Athens. Instead, they let it survive as a center of learning and intellectual influence, and science and philosophy continued to flourish. However, by about 100 - 200 B.C., power had become highly centralized in the "Hellenic States." Creative Greek science died out in parallel with this trend.
The Greek astronomers had access to a long tradition of accurate observations by the
Babylonians. Babylonian astronomy was remarkably similar in many ways to that of the Maya
(but was carried out two millennia earlier)
Very detailed observations over centuries, combined with sophisticated mathematics,
allowed the Babylonian astronomers to determine accurately the periods of the motions of
the planets, and to predict specific events such as when Venus would be farthest from the
sun 
. However, they had made no effort to probe
further, into underlying causes.
Greek astronomy was strongly influenced by the followers of Pythagoras, who felt that everything could be understood in terms of special numbers - they even invented a hidden Earth to raise the number of planets to the desired count. The Pythagoreans originated the idea that the planets moved on circular orbits and at constant speed.
 |
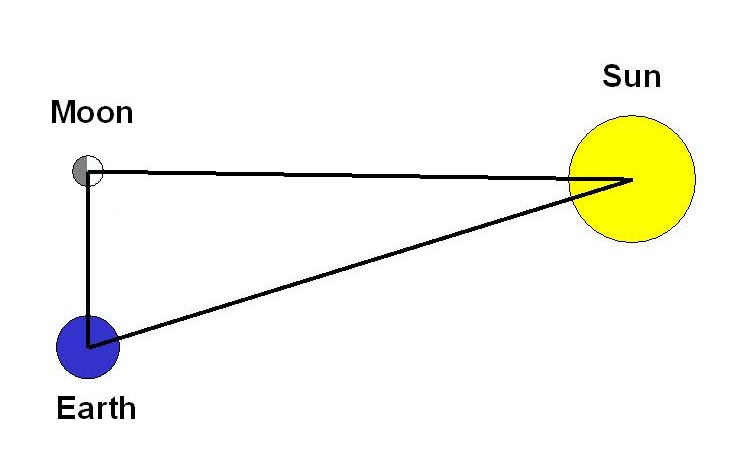An interesting issue was posed by Aristarchus (who lived about 280 B. C.). He attempted to measure the relative distances of the sun and moon by observing the angle between sun and moon when the moon is exactly half illuminated by the sun. He estimated the relative sizes of Earth and Moon from the shape of the shadow of the earth during lunar eclipses. Combining these results, he found that the sun was at least 300 times bigger in volume than the earth. Two centuries later, Posidonius made a new measurement of the size of the sun, finding it to be several thousand times the volume of the earth.(illustration by G. Rieke) |
If the sun were so much larger than the earth, Aristarchus argued that it was likely to lie at the center of the planetary system, with the earth orbiting it. He appreciated the issue of parallax in this system and correctly proposed that the stars are very far away compared with the size of the orbit of the earth: "that the sphere of fixed stars is of such a size that the circle, in which he supposes the earth to move, has the same ratio to the distance of the fixed stars as the center of a sphere has to the surface."
| Aristarchus also determined the distances from the earth to the moon and sun. He used a geometric argument based on how long lunar eclipses last plus his measurement of the relative sizes of the sun and moon to get the relative distances in terms of the sizes of the three bodies. He then applied Eratosthenes' measurement of the size of the earth to get distances in linear units. (animation by G. Rieke) |  |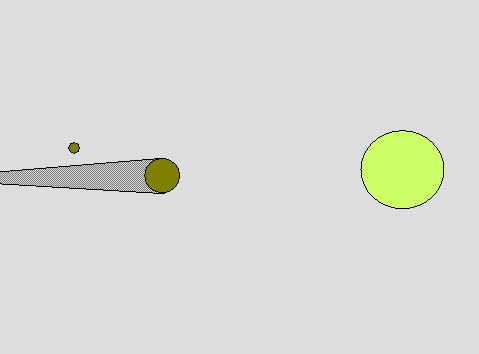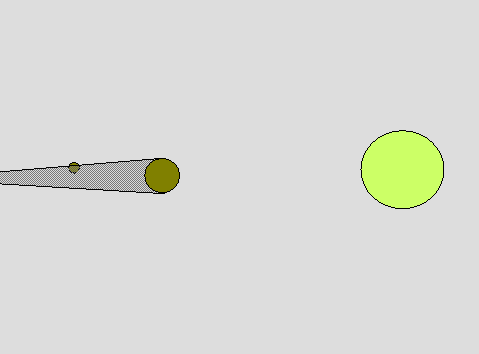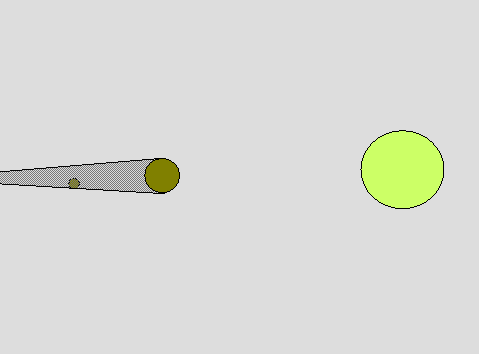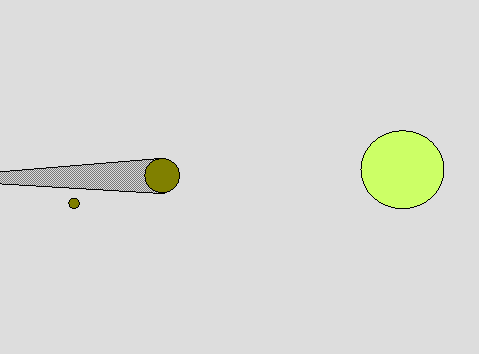
Despite the supporting observations regarding the size of the sun, Aristarchus' concept was ultimately rejected in favor of the purity of constant-rate circular motions. The reasons are not clear. It may have been that the conceptual difficulties with placing the stars so far away and the lack of any feeling of motion were too strong to overcome. A more interesting argument is that, as an astronomer, Aristarchus had little status in seeking underlying causes: astronomers were supposed just to observe and fit the motions of the planets and and it was the job of others, physicists, to find causes. Geminus, a commentator who is thought to have been inspired by the dominating late Greek scientist, Aristotle, stated: "For it is no part of the business of an astronomer to know what is by nature suited to a position of rest, and what sort of bodies are apt to move...But he must go to the physicist for his first principles." (de Santillana, p. 256). Even though his theory was not accepted, Aristarchus' work on the solar system is a model of the scientific approach - a startling new hypothesis that was backed up with observation and clever theory.
In many fields, the Greeks made great scientific advances that formed the foundation for modern understanding. In addition, the Greeks became obsessed with underlying causes. Many of these theories appear to us to be hopelessly naive, even fantastic, because their search for what lay underneath often seriously outstripped the Greeks' technology and they had no means to constrain their speculations by the type of precise, probing experiment modern science takes for granted. For example:
We should not give the Greeks too much credit when one of these theories (for example of atoms) anticipates a product of modern science. However, we must give immense credit for the pattern of thought that they introduced, the concept that things could be understood in terms of underlying causes and that these explanations could be tested to see if they were correct. These principles define the scientific method, as we still practice it. Their new method of thought has proven very powerful in making progress in our understanding of nature. Aristotle stated it more clearly than anyone since: "There is no science except of the general." (de Santillana, p. 210).