Some properties of ellipses:
 |
1. An ellipse has two points called foci (singular is
focus). In terms of the diagram, there is an “x” at each focus. The sum of the
distances from each focus for any point on the ellipse is equal to a constant value, e.g.
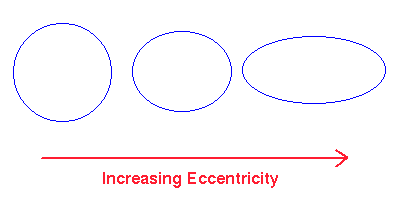
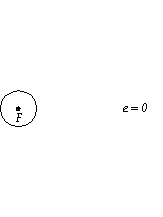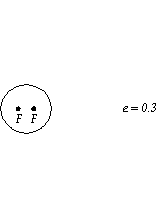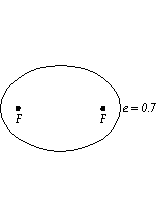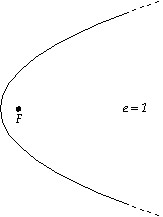a + b = Constant. 2. The amount of “flattening” of the ellipse is termed the eccentricity. In the following figure, the ellipses become more eccentric from left to right. A circle is a special case of an ellipse with zero eccentricity.(From U. Tenn, Ast. 161, http://csep10.phys.utk.edu/astr161/lect/history/kepler.html) |
 |
The orbits of most of the planets are so close to circular that it is difficult to tell the difference from a circle. The planets Mercury and Pluto have the largest eccentricities, followed by Mars. (Watch the eccentricity, with the value labelled "e", grow from 0 to 1 to the right.) From Scott Anderson, copyright open course, http://www.opencourse.info/ |  |
 |
The long axis of an ellipse is called the major axis and the short axis is called the minor axis. Half the major axis is called the semi-major axis. The semi-major axis becomes the radius in the case of a circle.(From U. Tenn, Ast. 161, http://csep10.phys.utk.edu/astr161/lect/history/kepler.html) |