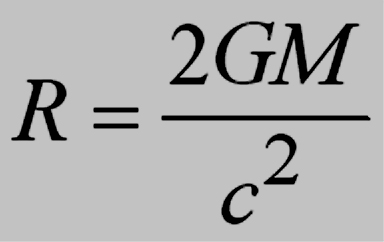Black Hole Stellar Remains

Key points: What a black hole is; event horizon; how we detect black holes

Some where between 3 and 5 M there is a limit on the sizes of neutron stars analogous to the 1.4M limit to white dwarfs. Stellar remnants larger than ~ 5M face yet another fate -- a black hole. The mass-size relationship for neutron stars is shown by the blue line. As mass gets added, the neutron star gets smaller, just as we also found for white dwarfs! When a neutron star gets so small it crosses the red line, it collapses into a black hole.

What is a black hole?

A black hole is an object whose escape velocity near its "surface" approaches the speed of light. The "surface" is called the event horizon as we are unable to observe anything inside this distance. This picture shows the light trajectories as a star gets closer and closer to the black hole. In (a), only a small portion of the light is directed close enough to the black hole to be captured. In (b), the star is close enough that the amount of light captured is increased because of the strong gravitational field of the black hole that bends the paths of the photons inward toward it. In (c), the star is much closer and this bending is so strong that fully half the light is captured. The amount of light captured goes up further as the star approaches closer, until in (d), nearly all of it does - just a little that happens to be emitted directly outward can get away. When the star gets still closer, no light gets out - it is then inside the event horizon. Nothing that happens inside the event horizon can be detected from outside, since no light (or anything else) can get out to show that something took place!! (from Dave Hanes, http://www.astro.queensu.ca/~hanes/p014/Notes/Topic_068.html)

We can estimate the size of the event horizon from the escape velocity

M = the mass of the central object; R = distance of orbiting object

At what R does the escape velocity = c , the speed of light?

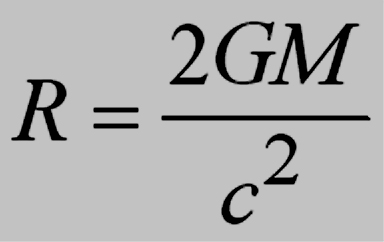
This R is called the Schwarzschild radius; it defines the position of the event horizon.

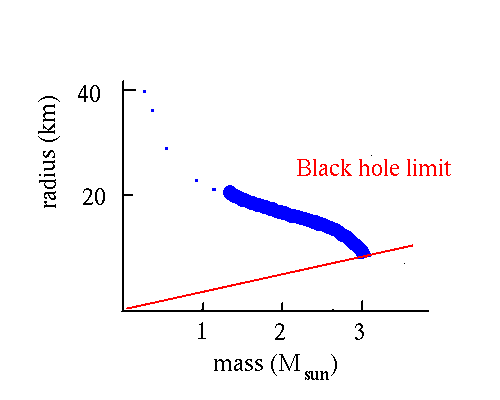
For an object with M = 6 M, R = 18 kilometers!

So black hole with a stellar type mass will have a "radius" of only a few tens of km, even smaller than a neutron star.

Close to the black hole, an improved theory of gravity, Einstein's General Theory of Relativity is needed to make calculations of how objects move; it would also slightly modify our calculation of where the event horizon is. The influence of gravity on light is included in this theory.

It predicts that time viewed from the outside will slow to a standstill as we watch something collapse into the event horizon, and that the photons it emits will be shifted progressively more and more to the red as they lose energy escaping from the huge gravitational field. Thus, if we could watch a star collapse into a  black hole, it might look like the simulation to the left. The infall seems to stop at the event horizon, where we get a frozen, dim red view of the surface of the dead star! Stellar remnant black holes are therefore sometimes called "frozen stars." (From Univ. Colorado, http://casa.colorado.edu/~ajsh/movies.html)

Einstein's theory states that if we were falling into the black hole, we would find no slowing down in time and would just plunge through the event horizon (and be torn apart  by tidal forces). Thus, the appearance of the collapse of the star depends completely on how and where we observe it

What happens if you are a some larger distance from a black hole?

Newton's Law of gravity will apply: F = GMm/r²

But you will probably be surprised to feel such a strong gravitational force from what may appear to be empty space! In fact, at first it may not be obvious where the black hole is (From R. Nemiroff, http://antwrp.gsfc.nasa.gov/htmltest/rjn_bht.html):

	It's over there! And we're getting closer.
	It becomes very obvious when we go into orbit around it -- look at the results of the light from background stars being deflected!

How do we know that these strange predictions by Einstein are correct and that light can be influenced by gravity? People looked for the "deflection" of starlight as it passed close to a massive object like the sun. The effect is seen exactly as Einstein's theory predicts it. Many other observations also support the theory. Einstein's theory is now virtually as secure as Newton's laws!Animation from Firstscience.com, http://www.firstscience.com/site/articles/einstein.asp

How do we look for stellar remnant black holes?

-- Look for x-ray emission

-- Although black holes are really black, when matter falls into them it can heat up so much it glows in x-rays

Gas pulled from the companion star into the gravitational field of the black hole heats up as it orbits inwards. The gas doesn't just fall straight in because of angular momentum -- the amount of rotational energy it has. The gas closest to the black hole can get so hot that it emits x-rays. The disk of gas is called an "accretion disk". (Illustration by Don Dixon; animation from J. Blondin http://wonka.physics.ncsu.edu/~blondin/AAS/)

One of the best examples is the apparently ordinary hot star HDE 22685. Not only is it a bright X-ray source, but it is a spectroscopic binary with an unseen companion with M > 3M, which is therefore likely to be a black hole. The system is shown to the left. (from Imagine the Universe, http://imagine.gsfc.nasa.gov/docs/science/know_l2/black_holes.html)

Another way to find black holes is to look for spectroscopic binaries where one star is invisible and where the velocities imply that a very massive object must be present (essentially the same as above but without the requirement that an "accretion disk" of hot gas be present).

Postage stamp celebrating Chandrasekhar's theory of white dwarfs		Simulation of effect of a nearby supernova on a star like the sun. http://www.pnl.gov/energyscience/
	Click to return to syllabus
Click to return to White Dwarfs and Neutron Stars	hypertext G. H. Rieke	Click to go to Novae and Supernovae