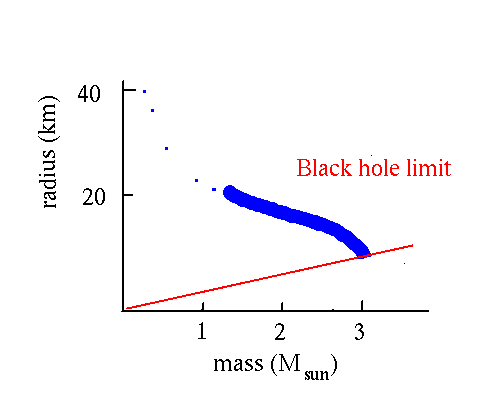
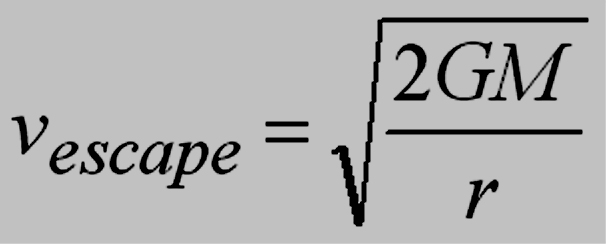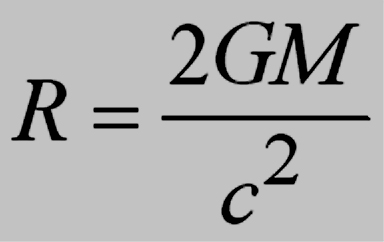Black Hole Stellar Remains
Key points: What a black hole is; event horizon; how we detect black holes
 |
Some where between 3 and 5 M there is a limit on the sizes of neutron
stars analogous to the 1.4M limit to
white dwarfs. Stellar remnants larger than ~ 5M face yet another fate -- a
black hole.The mass-size relationship for neutron stars is shown by the blue line. As mass gets added, the neutron star gets smaller, just as we also found for white dwarfs! When a neutron star gets so small it crosses the red line, it collapses into a black hole. |
| A black hole is an
object whose escape velocity near its "surface" approaches the speed of light.
The "surface" is called the event
horizon as we are unable to observe
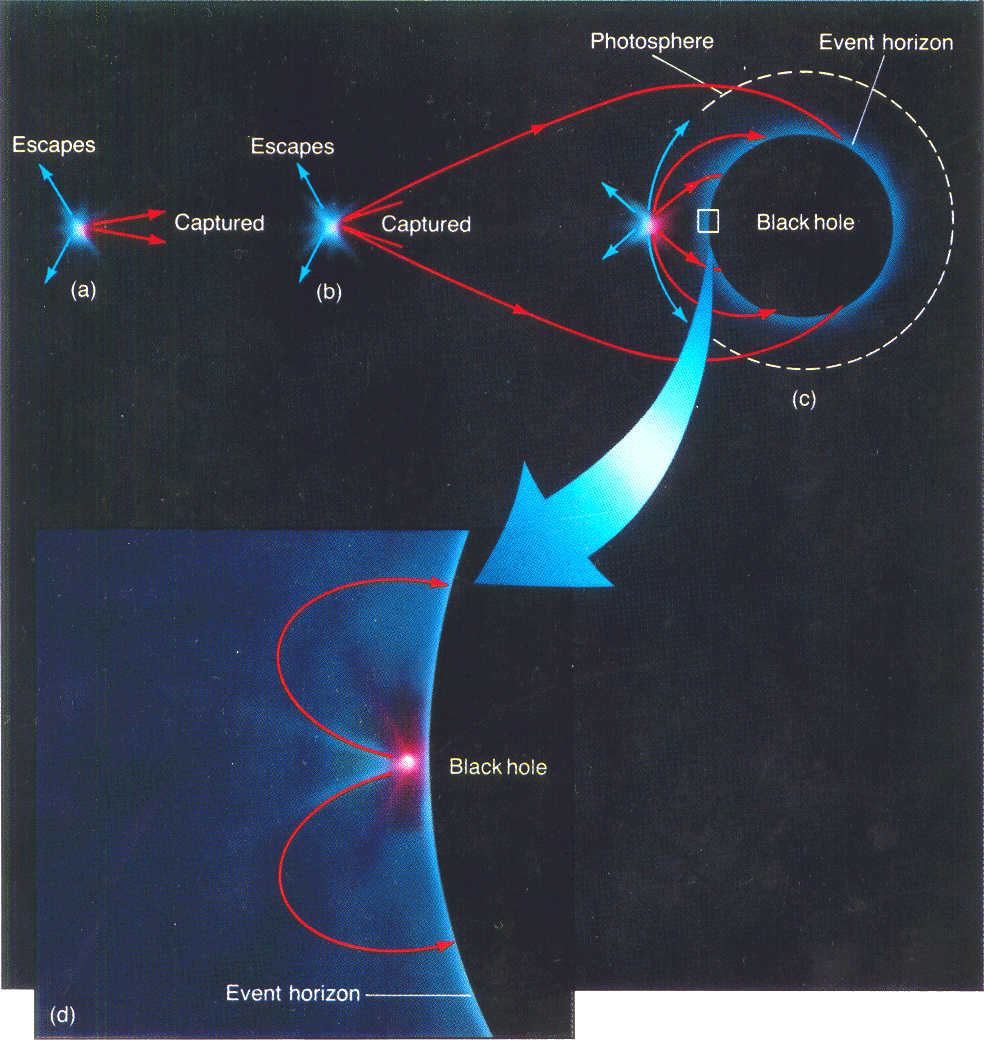
anything inside this distance. This picture shows the light trajectories as a star gets
closer and closer to the black hole. In (a), only a small portion of the light is directed
close enough to the black hole to be captured. In (b), the star is close enough that the
amount of light captured is increased because of the strong gravitational field of the
black hole that bends the paths of the photons inward toward it. In (c), the star is much
closer and this bending is so strong that fully half the light is captured. The amount of
light captured goes up further as the star approaches closer, until in (d), nearly all of
it does - just a little that happens to be emitted directly outward can get away. When the
star gets still closer, no light gets out - it is then inside the event horizon. Nothing
that happens inside the event horizon can be detected from outside, since no light (or
anything else) can get out to show that something took place!! (from Dave Hanes, http://www.astro.queensu.ca/~hanes/p014/Notes/Topic_068.html) Its a little like Las Vegas - only what happens in a black hole REALLY
stays there.
|
 |
We can estimate the size of the event horizon from the escape velocity
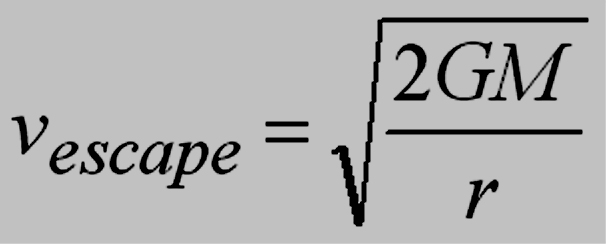
M = the mass of the central object; R = distance of orbiting object
At what R does the escape velocity = c , the speed of light?
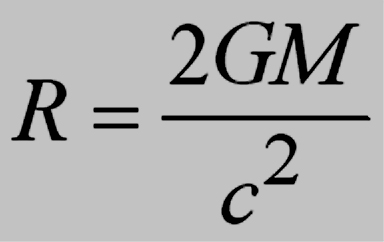
This R is called the Schwarzschild radius; it defines the position of the event horizon.
For an object with M = 6 M, R = 18 kilometers!
So a black hole with a stellar type mass will have a "radius" of only a few tens of km, even smaller than a neutron star.
Close to the black hole, an improved theory of gravity, Einstein's General Theory of Relativity is needed to make calculations of how objects move; it would also slightly modify our calculation of where the event horizon is. The influence of gravity on light is included in this theory.
 |
It predicts that time viewed from the outside will slow to
a standstill as we watch something collapse into the event horizon, and that the photons
it emits will be shifted progressively more and more to the red as they lose energy
escaping from the huge gravitational field. Thus, if we could watch a star collapse into a black hole, it might look like the simulation to the left. The infall seems to stop at the event horizon, where we get a frozen, dim red view of the surface of the dead star! Stellar remnant black holes are therefore sometimes called "frozen stars." (From Univ. Colorado, http://casa.colorado.edu/~ajsh/movies.html) |
Einstein's theory states that if we were falling into the black hole, we
would find no slowing down in time and would just plunge through the event horizon (and be
torn apart by tidal forces). Thus, the appearance of the collapse of the star
depends completely on how and where we observe it
What happens if you are a some larger distance from a black hole?
Newton's Law of gravity will apply: F = GMm/r2
But you will probably be surprised to feel such a strong gravitational force from what may appear to be empty space! In fact, at first it may not be obvious where the black hole is (From R. Nemiroff, http://antwrp.gsfc.nasa.gov/htmltest/rjn_bht.html):
 |
It's over there! And we're getting closer. |
 |
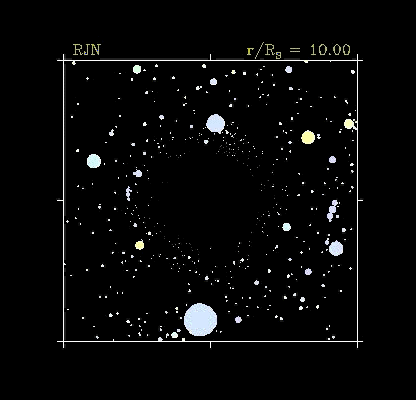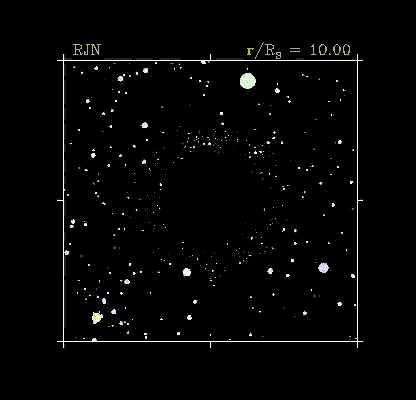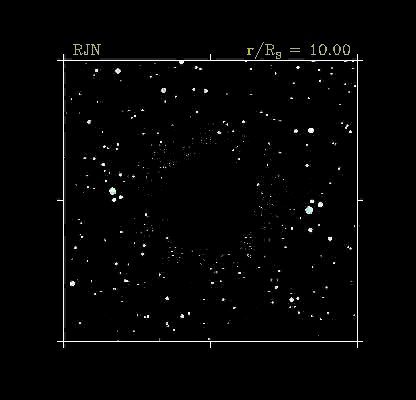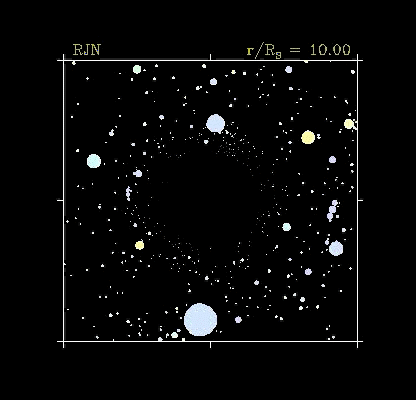It becomes very obvious when we go into orbit around it -- look at the results of the light from background stars being deflected! |
 |
How do we know that these strange
predictions by Einstein are correct and that light can be influenced by gravity?
People looked for the "deflection" of starlight as it
passed close to a massive object like the sun. The effect is seen exactly as Einstein's
theory predicts it. Einstein's theory is now virtually as secure as Newton's laws!Animation from Firstscience.com, http://www.firstscience.com/site/articles/einstein.asp |
 |
-- Look for x-ray emission
-- Although black holes are really black, when matter falls into them it can heat up so much it glows in x-rays
 |
Gas is pulled from the companion star into the gravitational field of the black hole. The gas doesn't just fall straight in because of angular momentum -- the amount of rotational energy it has around the black hole. As it orbits, it heats up due to friction against itself. The gas closest to the black hole can get so hot that it emits x-rays. The disk of hot gas is called an "accretion disk". (Illustration from ESO, http://ww.eso.org/public/outreach/press-rel/pr-2008/phot-36-08.html; animation from J. Blondin http://wonka.physics.ncsu.edu/~blondin/AAS/) |
 |
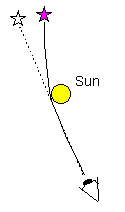
One of the best examples is what appears to
be an ordinary hot star, HDE
226868. However, it is a bright X-ray source, and an unseen companion orbits
it every 5.6 days. By applying the Newton/Kepler laws, the mass of the companion
is about 8.7M, so it is a black hole. Its gravitational pull on the star is
so great that it raises tides on the star that make it nearly 10% bigger
toward the black hole than it is in its other dimensions (measured from the
variations in the light it emits). The
system is shown to the left. (from Imagine the Universe, http://imagine.gsfc.nasa.gov/docs/science/know_l2/black_holes.html)
|
Postage stamp celebrating Chandrasekhar's theory of white dwarfs |
|
Simulation of effect of a nearby supernova on a star like the sun. http://www.pnl.gov/energyscience/
|
Click to return to syllabus |
||
| Click to return to White Dwarfs and Neutron Stars | hypertext |
Click to go to Novae and Supernovae |
G. H. Rieke